Graph Implementation in C Using Adjacency Matrix

Adjacency Matrices    There are several different ways to represent a graph in a computer.  Although graphs are usually shown diagrammatically, this is only possible when the number of vertices and edges is reasonably small.
    Graphs can also be represented in the form of matrices.  The major advantage of matrix representation is that the calculation of paths and cycles can easily be performed using well known operations of matrices. However, the disadvantage is that this form of representation takes away from the visual aspect of graphs.  It would be difficult to illustrate in a matrix, properties that are easily illustrated graphically.
 
Example:  Matrix representation of a graph
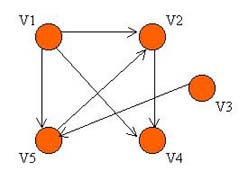
    Consider the following directed graph G (in which the vertices are ordered as v₁, v₂, v₃, v₄, and v₅), and its equivalent adjacency matrix representation on the right:

v1 v2 v3 v4 v5 v1 0 1 0 1 1 v2 0 0 0 1 0 v3 0 0 0 0 1 v4 0 0 0 0 0 v5 0 1 0 0 0

    As you can see from the above graph, if a path of length 1 exists from one vertex to another (ie. the two vertices are adjacent), there must be an entry of 1 in the corresponding position in the matrix.  For example, from the vertex v1, we can reach vertices v2, v4, and v5. Therefore, we have a corresponding entry of 1 in the matrix in the first row and the second, fourth and fifth columns.
    In general, the number of 1's in the ith row, corresponds to the number of edges leaving the vertex v_i, and the number of 1's in the jth column, corresponds to the number of edges entering the vertex v_j.
 
Definition of an Adjacency Matrix
    An adjacency matrix is defined as follows:  Let G be a graph with "n" vertices that are assumed to be ordered from v₁ to v_n.
The n x n matrix A, in which
           a_ij= 1        if there exists a path from v_i to v_j
            a_ij = 0        otherwise
is called an adjacency matrix.

Graph Traversal

14.1 Depth-First Traversal

algorithm  dft(x) 
   visit(x) 
   FOR each y such that (x,y) is an edge DO 
     IF y was not visited yet THEN 
        dft(y) 

A recursive algorithm implicitly recording a “backtracking” path from the root to the node currently under consideration

14.2 Breadth-First Traversal

Visit the nodes at level i before the nodes of level i+1.

visit(start node) 
queue <- start node 
WHILE queue is nor empty DO 
  x <- queue 
  FOR each y such that (x,y) is an edge 
                  and y has not been visited yet DO 
    visit(y) 
    queue <- y 
  END 
END 

Implementation in C

#include stdio.h
#include stdlib.h

#define MAX 20

typedef enum boolean{false,true} bool;
int adj[MAX][MAX];
bool visited[MAX];
int n;    /* Denotes number of nodes in the graph */

void create_graph()
{
    int i,max_edges,origin,destin;

    printf("Enter number of nodes : ");
    scanf("%d",&n);
    max_edges=n*(n-1);

    for(i=1;i<=max_edges;i++)
    {
        printf("Enter edge %d( 0 0 to quit ) : ",i);
        scanf("%d %d",&origin,&destin);

        if((origin==0) && (destin==0))
            break;

        if( origin > n || destin > n || origin<=0 || destin<=0)
        {
            printf("Invalid edge!\n");
            i--;
        }
        else
        {
            adj[origin][destin]=1;
        }
    }/*End of for*/
}/*End of create_graph()*/

void display()
{
    int i,j;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
            printf("%4d",adj[i][j]);
        printf("\n");
    }
}/*End of display()*/

void dfs(int v)
{
    int i;
    visited[v]=true;
    printf("%d ",v);
    for(i=1;i<=n;i++)
        if(adj[v][i]==1 && visited[i]==false)
            dfs(i);
}/*End of dfs_rec()*/


void bfs(int v)
{
    int i,front,rear;
    int que[20];
    front=rear= -1;

    printf("%d ",v);
    visited[v]=true;
    rear++;
    front++;
    que[rear]=v;

    while(front<=rear)
    {
        v=que[front];     /* delete from queue */
        front++;
        for(i=1;i<=n;i++)
        {
            /* Check for adjacent unvisited nodes */
            if( adj[v][i]==1 && visited[i]==false)
            {
                printf("%d ",i);
                visited[i]=true;
                rear++;
                que[rear]=i;
             }
        }
    }/*End of while*/
}/*End of bfs()*/

int main()
{
    int i,v,choice;

    create_graph();
    while(1)
    {
        printf("\n");
        printf("1. Adjacency matrix\n");
        printf("2. Depth First Search\n");
        printf("3. Breadth First Search\n");
        printf("4. Exit\n");
        printf("Enter your choice : ");
        scanf("%d",&choice);

        switch(choice)
        {
         case 1:
            printf("Adjacency Matrix\n");
            display();
            break;
         case 2:
            printf("Enter starting node for Depth First Search : ");
            scanf("%d",&v);
            for(i=1;i<=n;i++)
                visited[i]=false;
            dfs(v);
            break;
         case 3:
            printf("Enter starting node for Breadth First Search : ");
            scanf("%d", &v);
            for(i=1;i<=n;i++)
                visited[i]=false;
            bfs(v);
            break;
       
         case 4:
            exit(1);
         default:
            printf("Wrong choice\n");
            break;
         }/*End of switch*/
    }/*End of while*/
return 0;
}/*End of main()*/

Output

sarju@sarju-HP-Pavilion-g6-Notebook-PC:~$ gcc -Wall graph.c
sarju@sarju-HP-Pavilion-g6-Notebook-PC:~$ ./a.out
Enter number of nodes : 5
Enter edge 1( 0 0 to quit ) : 1 2
Enter edge 2( 0 0 to quit ) : 1 3
Enter edge 3( 0 0 to quit ) : 2 4
Enter edge 4( 0 0 to quit ) : 3 5
Enter edge 5( 0 0 to quit ) : 0 0

1. Adjacency matrix
2. Depth First Search
3. Breadth First Search
4. Exit
Enter your choice : 1
Adjacency Matrix
   0   1   1   0   0
   0   0   0   1   0
   0   0   0   0   1
   0   0   0   0   0
   0   0   0   0   0

1. Adjacency matrix
2. Depth First Search
3. Breadth First Search
4. Exit
Enter your choice : 2
Enter starting node for Depth First Search : 1
1 2 4 3 5
1. Adjacency matrix
2. Depth First Search
3. Breadth First Search
4. Exit
Enter your choice : 3
Enter starting node for Breadth First Search : 1
1 2 3 4 5
1. Adjacency matrix
2. Depth First Search
3. Breadth First Search
4. Exit
Enter your choice : 4
sarju@sarju-HP-Pavilion-g6-Notebook-PC:~$